EMG-Filter
Auf jede Spur in jedem Fenster können bis zu sechs Filtereffekte angewendet werden. Die Originaldaten werden dem ersten aktivierten Filter unterzogen. Die Ausgabe dieses Filters wird dem nächsten aktivierten Filter unterzogen und so weiter bis zu maximal sechs Filtern. Die Ausgabe des Endfilters wird angezeigt.
Jeder der Filter hat die folgenden Optionen:
Dieser Filter konvertiert einfach einen negativen Wert in einen positiven Wert gleicher Größe. Es ist keine Filterkonstante erforderlich.
Ein Gleitender-Mittelwert-Filter kann auf jede Wellenform angewendet werden.
- Wenn aktiviert, ist jeder in einer Messkurve berechnete Punkt der Mittelwert einer Anzahl von Werten bis einschließlich des aktuellen Punktes.
- Die Anzahl der Werte ist die Filterkonstante und kann von 2 Messwerten aufwärts eingestellt werden.
- Die Filterkonstante kann in Messwerten oder Millisekunden angegeben werden, wobei die Anzahl der Millisekunden die Anzahl der Samples multipliziert mit (1000/Sampling Rate) ist.
- Der gleitende Mittelwert erzeugt so viele Ausgänge wie Eingänge. Bei einer Filterkonstante von z. B. 3 ergeben sich folgende Berechnungen:
- Ausgang 1 = Eingang 1
- Ausgang 2 = Mittelwert der Eingänge 1 und 2
- Ausgang 3 = Mittelwert der Eingänge 1,2 und 3
- Ausgang 4 = Mittelwert der Eingänge 2,3 und 4
- Ausgang 5 = Mittelwert der Eingänge 3,4 und 5
- Ausgang n = Mittelwert der Eingänge n-2, n-1 und n
HINWEIS: Der Mittelwertfilter ist nützlich, um hochfrequentes Rauschen in einer Wellenform zu reduzieren. Enthält z. B. eine bei 1000 Hz abgetastete Herzschlagkurve 50 Hz Netzstörung, kann sie durch Mittelwertbildung über einen Netzzyklus (1/50. Sekunde) reduziert werden. Ein Netzzyklus entspricht 20 Abtastwerten (1000 Hz Abtastrate geteilt durch 50 Hz Interferenz), so dass eine Mittelung von 20 Werten das Rauschen deutlich reduziert. Beachten Sie, dass eine Mittelwertbildung über 40,60,80, ... Messwerte auch das Rauschen reduziert, aber es kann auch das interessierende Signal reduzieren.
Jede Stichprobe von Daten wird zuerst quadriert und dann wird ein gleitender Durchschnitt dieser Quadrate genommen. Die Ausgabe ist die Quadratwurzel jedes berechneten Durchschnitts.
- Die Filterkonstante kann in Samples oder Millisekunden angegeben werden, wobei die Anzahl der Millisekunden die Anzahl der Messwerte multipliziert mit (1000/Abtastrate) ist.
Der Geschwindigkeitsfilter berechnet die Änderungsgeschwindigkeit der Daten an jedem Datenpunkt. Dies ist praktisch die Steigung der Tangente zur Linie an diesem Punkt.
Um einen geeigneten Gradienten zu erhalten, wird eine Geradenschätzung mit Hilfe der Methode der kleinsten Quadrate auf beiden Seiten des zu berechnenden Datenpunkts durchgeführt. Der Gradient dieser Linie ist der Filterausgang.
- Die Filterkonstante definiert die Anzahl der Datenpunkte, die bei der Abschätzung mittels der Methode der kleinsten Quadrate verwendet werden. Sie kann in Samples oder Millisekunden angegeben werden, wobei die Anzahl der Millisekunden die Anzahl der Messwerten multipliziert mit (1000/Sampling Rate) ist.
- Mit diesem Filter werden die angezeigten Einheiten verändert. Wenn z. B. die ursprünglichen Einheiten Grad sind, werden die gefilterten Einheiten Grad/Sekunden sein.
Der Integralfilter berechnet den Bereich unter der Graphik vom Start bis zum angezeigten Punkt. Dieser Filter erzeugt oft eine schnell ansteigende/abfallende Grafik, wenn die Daten nicht auf Null zentriert sind.
- Die Filterkonstante definiert einen Teiler, der die berechnete Fläche für jeden Punkt reduziert. Dies ist nützlich, wenn die Daten ansonsten eine Integralausgabe erzeugen würden, die zu groß ist, um sie anzuzeigen.
- Mit diesem Filter werden die angezeigten Einheiten verändert. Wenn z. B. die ursprünglichen Einheiten Grad sind, dann werden die gefilterten Einheiten Grad-Sekunden sein.
Der Offsetfilter addiert oder subtrahiert einfach einen Prozentsatz des Endwertes von jedem Datenpunkt. Damit kann der Null- oder Nullpunkt für jede Messkurve geändert oder neu definiert werden. Dies hat den Effekt, dass die Messkurve im Fenster nach oben oder unten bewegt wird.
- Die Filterkonstante definiert den Prozentsatz der Skalenendwerte und kann positiv oder negativ sein.
Der Skalenfilter multipliziert einfach jeden Datenpunkt mit einem Prozentsatz der Skalenendwerte. Dies hat den Effekt, dass die Größe einer Messkurve im Fenster vergrößert oder verkleinert wird.
- Die Filterkonstante definiert den Prozentsatz des ursprünglichen Wertes. Konstanten kleiner als 100% reduzieren die Amplitude der Messkurve, während Konstanten größer als 100% die Amplitude der Messkurve erhöhen.
Die mittlere Frequenz wird für einen Block von Messwerten berechnet, dessen Länge durch die Filterkonstante definiert ist. Diese Berechnung wird bei Bedarf über die Messkurve hinweg wiederholt und die resultierenden Frequenzen als eine Reihe von Linien aufgetragen, die die berechneten mittleren Frequenzen verbinden. Die folgenden Schritte werden ausgeführt:
- Ein durch die Filterkonstante definierter Block von Messwerten wird entnommen und der Nullpunkt auf die nächstmögliche Zweierpotenz aufgefüllt.
- Eine Fensterfunktion, die auf die Daten angewendet wird, wie durch die Auswahl unten links im Einstellungsfenster festgelegt. Weitere Informationen finden Sie unter FFT-Fensterfunktionen verwenden.
- Eine FFT wird ausgeführt und, wenn ausgewählt, werden FFT-Hochpassfilter verwendet, um DC zu entfernen und sehr niedrige Frequenzen aus den Berechnungen zu entfernen. Beachten Sie, dass eine große DC-Komponente die Genauigkeit der Mittelfrequenzberechnung stark beeinträchtigen kann.
- Die Amplitudengröße jeder FFT-Ausgangsfrequenz wird quadriert.
- Die mittlere Frequenz wird so bestimmt, daß die Fläche des Amplituden-Quadrat-Frequenzgraphen unterhalb der mittleren Frequenz die gleiche ist wie oberhalb der mittleren Frequenz, d. h. es gibt auf beiden Seiten der mittleren Frequenz gleiche Leistung.
- Der Vorgang wird für den nächsten Block von Messwerten wiederholt.
Die mittlere Frequenz wird für einen Block von Messwerten berechnet, dessen Länge durch die Filterkonstante definiert ist. Diese Berechnung wird bei Bedarf über die Messkurve wiederholt und die resultierenden Frequenzen als eine Reihe von Linien aufgetragen, die die berechneten Mittelfrequenzen verbinden. Die folgenden Schritte werden ausgeführt:
- Ein durch die Filterkonstante definierter Block von Messwerten wird entnommen und der Nullpunkt auf die nächstmögliche Zweierpotenz aufgefüllt.
- Eine Fensterfunktion, die auf die Daten angewendet wird, wie durch die Auswahl unten links im Einstellungsfenster festgelegt. Weitere Informationen finden Sie unter “FFT-Fensterfunktionen verwenden”.
- Eine FFT wird ausgeführt und, wenn ausgewählt, werden FFT-Hochpassfilter verwendet, um DC und sehr niedrige Frequenzen aus den Berechnungen zu entfernen. Beachten Sie, dass eine große DC-Komponente die Genauigkeit der Mittelfrequenzberechnung stark beeinträchtigen kann.
- Es wird eine FFT durchgeführt und alle Frequenzen unterhalb (einer maximalen Frequenz / 50) Hz werden verworfen; dies entspricht 10Hz bei 1000 Proben / Sekunde.
- Die Amplitudengröße jeder FFT-Ausgangsfrequenz wird quadriert.
- Die mittlere Frequenz des resultierenden Amplitudenquadrats zum Frequenzgang wird bestimmt.
- Der Vorgang wird für den nächsten Block von Messwerten wiederholt.
Wenn Daten erfasst werden, wird ein "Fenster" auf dem Signal geöffnet, um die Wellenform für eine Zeitspanne zu betrachten, bevor das "Fenster" wieder geschlossen wird. Vor und nach dem Öffnen des Fensters hat die FFT-Berechnung keine Kenntnis vom Signalwert. Beispielsweise enthalten die vier rechts abgebildeten Wellenformen dieselben (in Grau dargestellten) aufgezeichneten Daten, haben aber unterschiedliche Frequenzinhalte.
Eine FFT geht davon aus, dass die Datenfolge Teil eines Signals ist, das sich periodisch wiederholt, wie durch die Sägezahnwellenform rechts unten im obigen Diagramm veranschaulicht. Die Folge der Annahme einer periodischen Fortsetzung des zugrunde liegenden Signals ist, dass, wenn die Amplitude am Anfang und am Ende der Abtastung nicht gleich ist, das Signal analysiert wird, um eine Diskontinuität zu erhalten, unabhängig davon, ob das Signal eine solche Diskontinuität aufweist oder nicht. Da scharfe Diskontinuitäten breite Frequenzspektren haben, wird das Frequenzspektrum des Signals durch diese breit gestreut. Die Streuung bedeutet, dass die Signalenergie, die nur auf eine Frequenz konzentriert werden sollte, stattdessen in alle anderen Frequenzen austritt. Diese Energieverteilung wird als Leck-Effekt bezeichnet. Da spektrale Leckage mit Diskontinuitäten am Ende der Messzeit zusammenhängt, wird es für Signale, die zufällig fallen, schlechter sein, so dass es große Diskontinuitäten gibt
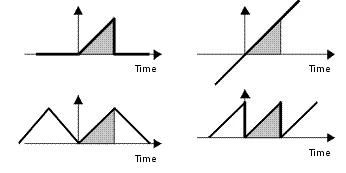
This is a problem since the FFT will only be an accurate calculation of the frequency content if the captured data is one or more complete cycles of a periodic underlying signal. This is normally not the case.
In order to improve the accuracy of the FFT, it is normal practice to multiply the sampled data by a window function before implementing the FFT. This window function is a series of numbers that are usually symmetrical with the mid-point of the sample time range and have a mid-point value of one e.g. the Triangle or Bartlett window.

A number of window functions are possible including a Rectangular Window that does not actually change the data at all. Some of the window functions provided are:
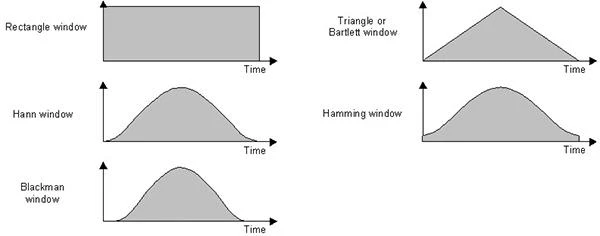
In order to compare the different windows, they may be plotted on the same axis as follows:
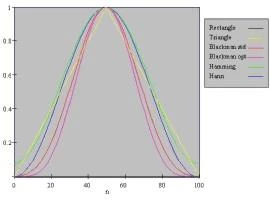
Die Wahl der Fensterfunktion erfolgt in der Regel nach einiger Erfahrung mit der Verarbeitung der verwendeten Signalart. Es können jedoch einige Richtlinien vorgegeben werden:
- Rechteckfenster für kurzzeitige Signale verwenden;
- Hann (von Hann) und Hamming für kontinuierliche Wellenformdaten;
- Rechteckig (Flat-Top) für genaue Amplitudenmessungen oder
- Blackman für maximale Frequenz-Auflösung
