Filtres EMG

Un filtre de moyenne mobile peut être appliqué à toute forme d'onde.

• Lorsqu'il est activé, chaque point calculé dans la courbe est la moyenne d'un certain nombre de valeurs précédent le point actuelet lui même.
• La constante du filtre correspond au nombre de valeur à prendre en compte dans la moyenne. Le réglage le plus petit est 2.
• La constante du filtre peut être spécifiée en échantillons ou en millisecondes, le nombre de millisecondes étant le nombre d'échantillons multiplié par (1000/fréquence d'échantillonnage).
• La moyenne mobile génère autant de résultats que d'entrées. Par exemple, en supposant une constante de filtre de 3, les calculs suivants sont effectués :
  • Sortie 1 = Entrée 1
  • Sortie 2 = Moyenne des entrées 1 et 2
  • Sortie 3 = Moyenne des entrées 1, 2 et 3
  • Sortie 4 = Moyenne des entrées 2, 3 et 4
  • Sortie 5 = Moyenne des entrées 3, 4 et 5
  • Sortie n = Moyenne des entrées n-2, n-1 et n

ASTUCE : Le filtre moyen est utile pour réduire le bruit de haute fréquence d’une onde. Par exemple, si un tracé de battement cardiaque échantillonné à 1000 Hz contient des interférences de 50 Hz, celles-ci peuvent être réduites en faisant la moyenne sur un cycle (1/50ème de seconde). Un cycle correspond à 20 échantillons (fréquence d'échantillonnage de 1000 Hz divisée par l'interférence de 50 Hz) ; le calcul de la moyenne de 20 valeurs réduira donc le bruit de manière significative. Notez que le calcul de la moyenne sur 40, 60, 80, ... échantillons réduira également le bruit mais aussi le signal.

Chaque échantillon de données est d'abord élevé au carré, puis une moyenne mobile est calculée à partir de ces carrés. Le résultat de sortie est la racine carrée de chaque moyenne calculée.

• La constante du filtre peut être spécifiée en échantillons ou en millisecondes, le nombre de millisecondes étant le nombre d'échantillons multiplié par (1000/fréquence d'échantillonnage).

Le filtre de vélocité consiste à calculer le taux de changement des données à chaque point de données. Il s'agit en fait du gradient de la tangente à la ligne à ce point.

Pour obtenir un gradient approprié, une méthode des moindres carrés est utilisée pour estimer une ligne droite en utilisant les données de part et d'autre du point de données calculé. Le gradient de cette ligne correspond au résultat de sortie du filtre.

• La constante du filtre définit le nombre de points de données utilisés dans l'estimation de la ligne par la méthode des moindres carrés. Elle peut être spécifiée en échantillons ou en millisecondes, le nombre de millisecondes étant le nombre d'échantillons multiplié par (1000/taux d'échantillonnage).
• L'utilisation de ce filtre modifiera les unités affichées. Par exemple, si les unités d'origine sont les degrés, les unités filtrées seront les degrés/seconde.

Le filtre d'intégration calcule l'aire sous la courbe, cela depuis le début jusqu'au point affiché. Ce filtre produit souvent un graphique qui augmente ou diminue rapidement lorsque les données ne sont pas centrées autour de zéro.

• La constante du filtre définit un diviseur utilisé pour réduire l'aire calculée pour chaque point. Ceci est utile lorsque les données produiraient autrement une sortie intégrée trop grande pour être affichée
• L'utilisation de ce filtre modifiera les unités affichées. Par exemple, si les unités d'origine sont les degrés, les unités filtrées seront les degrés-sec.

Le filtre de décalage ajoute ou soustrait simplement un pourcentage de l’ échelle à chaque point des données. Il peut être utilisé pour modifier ou redéfinir le point nul ou zéro de chaque courbe. Cela a pour effet de déplacer la courbe vers le haut ou vers le bas de la fenêtre.

• La constante du filtre définit le pourcentage de l’échelle à ajouter ou à soustraire et peut être positive ou négative.

Le filtre d'échelle multiplie chaque données par un pourcentage de l’échelle. Cela a pour effet d'augmenter ou de diminuer la taille d'une courbe dans la fenêtre.

• La constante du filtre définit le pourcentage de la valeur d'origine. Les constantes inférieures à 100 % réduisent l'amplitude de la courbe, tandis que les constantes supérieures à 100 % augmentent l'amplitude de la courbe.

La fréquence médiane est calculée pour un ensemble de données. La taille de cet échantillon est définie par la constante du filtre. Ce calcul est répété autant que nécessaire tout au long de la courbe et les fréquences résultantes sont tracées comme une série de droites reliant les fréquences médianes calculées. Les étapes suivantes sont réalisées pour obtenir ce résultat :

• Un bloc d'échantillons défini par la constante du filtre est prélevé et mis à zéro à la puissance de 2 la plus proche.
• Une fonction de fenêtrage est appliquée aux données comme spécifié par la sélection en bas à gauche de la fenêtre Paramètre. Allez dans la section utilisation des fonctions de fenêtrage FFT pour plus d'informations.
• Une FFT est effectuée et, si cette option est sélectionnée, des filtres passe-haut FFT sont utilisés pour éliminer le courant continu et les très basses fréquences des calculs. Notez qu'une composante DC importante peut sérieusement dégrader la précision du calcul de la fréquence médiane.
• La magnitude de l'amplitude de chaque fréquence de sortie de la FFT est élevée au carré.
• La fréquence médiane est déterminée de telle sorte que l’aire du graphique de l'amplitude au carré de la fréquence située en dessous de la fréquence médiane soit la même que l’air située au-dessus de la fréquence médiane. C'est-à-dire qu'il y a une force égale de part et d'autre de la fréquence médiane.
• Le processus est répété pour le bloc d'échantillons suivant.

La fréquence moyenne est calculée pour un ensemble de données. La taille de cet échantillon est définie par la constante du filtre. Ce calcul est répété autant que nécessaire tout au long de la courbe et les fréquences résultantes sont tracées comme une série de droites reliant les fréquences moyenne calculées. Les étapes suivantes sont réalisées pour obtenir ce résultat:

• Un bloc d'échantillons défini par la constante du filtre est prélevé et mis à zéro à la puissance 2 la plus proche.
• Une fonction de fenêtrage est appliquée aux données comme spécifié par la sélection en bas à gauche de la fenêtre Paramètre. Allez dans la section utilisation des fonctions de fenêtrage FFT pour plus d'informations.
• Une FFT est effectuée et, si cette option est sélectionnée, des filtres passe-haut FFT sont utilisés pour éliminer le courant continu et les très basses fréquences des calculs. Notez qu'une composante DC importante peut sérieusement dégrader la précision du calcul de la fréquence moyenne.
• Une FFT est effectuée et toutes les fréquences inférieures à (fréquence maximale / 50) Hz sont rejetées ; cela correspond à 10Hz à 1000 échantillons / seconde.
• L'amplitude de chaque fréquence de sortie de la FFT est élevée au carré.
• La fréquence moyenne résultant de l'amplitude élevée au carré par rapport à la fréquence du graphique est déterminée.
• Le processus est répété pour le bloc d'échantillons suivant.

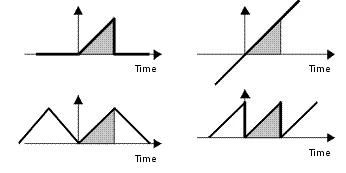
Lorsque des données sont enregistrés, une "fenêtre d’observation" est ouverte sur le signal pour visualiser la courbe pendant un certain temps avant que la "fenêtre d’observation" ne soit refermée. Avant et après l'ouverture de la fenêtre, le calcul FFT ne connait pas la valeur du signal. Par exemple, les quatre formes d'onde illustrées à droite contiennent les mêmes données capturées (en gris) mais ont des contenus fréquentiels différents.

Une FFT suppose que la séquence de données fait partie d'un signal qui se répète périodiquement, comme l'illustre l'onde en dents de scie en bas à droite ci-dessus. La conséquence de l'hypothèse d'une continuation périodique du signal sous-jacent est que si l'amplitude au début et à la fin de l'échantillon de données n'est pas égale, le signal sera analysé comme contenant une discontinuité, peu importe que ce soit le cas ou non. Comme les discontinuités nettes ont des spectres de fréquence larges, elles provoquent un étalement du spectre de fréquence du signal. Cet étalement signifie que l'énergie du signal, qui devrait être concentrée sur une seule fréquence, s'infiltre dans toutes les autres fréquences. Cet étalement de l'énergie est appelé "fuite spectrale". Comme la fuite spectrale est liée aux discontinuités à la fin du temps de mesure, elle sera plus importante pour les signaux qui s’arrête en causant de grosses discontinuités.

C'est un problème car la FFT ne sera un calcul précis du contenu des fréquence que si les données capturées sont prises sur un ou plusieurs cycles complets d'un signal périodique sous-jacent. Cela n'est normalement pas le cas.

Pour améliorer la précision de la FFT, il est courant de multiplier les données échantillonnées par une fonction de fenêtre avant d’appliquer la FFT. Cette fonction fenêtre est une série de nombres qui sont généralement symétriques par rapport au point médian de la plage de temps d'échantillonnage et dont la valeur du point médian est de un, par exemple la fenêtre Triangle ou Bartlett.

De nombreuses fonctions de fenêtre sont possibles, y compris une fenêtre rectangulaire qui ne modifie pas les données. Voici quelques-unes des fonctions de fenêtre proposées :

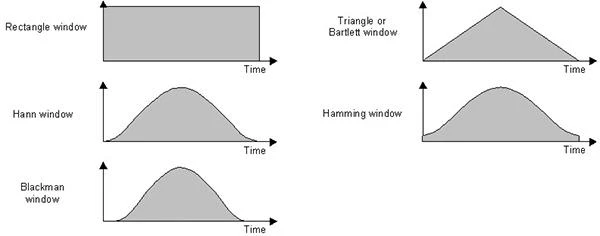
Pour comparer les différentes fenêtres, on peut les tracer sur le même axe comme suivant :

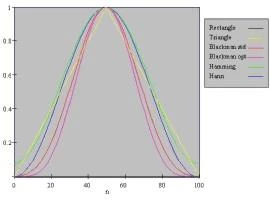
Le choix de la fonction fenêtre devient plus simple lorsqu’on accquiert une certaine expérience dans le traitement de ce type de signaux. Cependant, voici quelques recommandations:

• Utilisez une fenêtre rectangulaire pour les signaux transitoires ;
• Utilisez Hann (von Hann) et Hamming pour les ondes continues ;
• Rectangulaire (Flattop) pour des mesures d'amplitude précises ou
• Blackman pour une résolution de la fréquence maximale.