Filtros EMG
Todo rastreamento em cada janela pode ter até seis efeitos de filtro aplicados. Os dados originais são submetidos ao primeiro filtro ativado. A saída desse filtro está sujeita ao próximo filtro ativado e assim por diante, até um máximo de seis filtros. A saída do filtro final é exibida.
Cada um dos filtros possui as seguintes opções:
Esse filtro simplesmente converte um valor negativo em um valor positivo da mesma magnitude. Nenhuma constante de filtro é necessária.
Um filtro de média móvel pode ser aplicado a qualquer forma de onda.
- Quando ativado, cada ponto calculado em um rastreamento é a média de um número de valores até e incluindo o ponto atual.
- O número de valores é a constante do filtro e pode ser definido de 2 amostras para cima.
- A constante do filtro pode ser especificada em amostras ou milissegundos em que o número de milissegundos é o número de amostras multiplicadas por (taxa de 1000 / amostragem).
- A média móvel gera tantas saídas quanto entradas. Por exemplo, assumindo uma constante de filtro 3, os seguintes cálculos são realizados:
- Saída 1 = Entrada 1
- o Saída 2 = Média das entradas 1 e 2
- o Saída 3 = Média das entradas 1, 2 e 3
- o Saída 4 = Média das entradas 2, 3 e 4
- o Saída 5 = Média das entradas 3, 4 e 5
- o Saída n = Média das entradas n-2, n-1 en
DICA: O filtro médio é útil para reduzir o ruído de alta frequência em uma forma de onda. Por exemplo, se um traço de batimento cardíaco amostrado em 1000Hz contiver 50Hz de interferência da rede elétrica, ele poderá ser reduzido pela média de um ciclo da rede elétrica (1/50 de segundo). Um ciclo de rede corresponde a 20 amostras (taxa de amostragem de 1000Hz dividida por interferência de 50Hz), de modo que a média de 20 valores reduzirá significativamente o ruído. Observe que a média de mais de 40, 60, 80 ,… amostras também reduzirá o ruído, mas também poderá reduzir o sinal de interesse.
Cada amostra de dados é primeiro ao quadrado e, em seguida, é obtida uma média móvel desses quadrados. A saída é a raiz quadrada de cada média calculada.
- A constante do filtro pode ser especificada em amostras ou milissegundos em que o número de milissegundos é o número de amostras multiplicadas por (taxa de 1000 / amostragem).
O filtro de velocidade envolve o cálculo da taxa de alteração dos dados em cada ponto de dados. Este é efetivamente o gradiente da tangente à linha naquele ponto.
Para obter um gradiente adequado, um método de mínimos quadrados é usado para estimar uma linha reta usando os dados de ambos os lados do ponto de dados que está sendo calculado. O gradiente desta linha é a saída do filtro.
- A constante de filtro define o número de pontos de dados usados na estimativa da linha dos mínimos quadrados. Pode ser especificado em amostras ou milissegundos em que o número de milissegundos é o número de amostras multiplicadas por (taxa de 1000 / amostragem).
- O uso deste filtro alterará as unidades exibidas. Por exemplo, se as unidades originais forem graus, as unidades filtradas serão graus / s.
O filtro de integração calcula a área sob o gráfico desde o início até o ponto que está sendo exibido. Esse filtro geralmente produz um gráfico que aumenta / diminui rapidamente quando os dados não estão centrados no zero.
- A constante de filtro define um divisor usado para reduzir a área calculada para cada ponto. Isso é útil quando os dados produzem uma saída de integração que é muito grande para ser exibida.
- O uso deste filtro alterará as unidades exibidas. Por exemplo, se as unidades originais forem graus, as unidades filtradas serão graus-segundo.
O filtro de deslocamento simplesmente adiciona ou subtrai uma porcentagem da escala completa de todos os pontos de dados. Isso pode ser usado para alterar ou redefinir o ponto nulo ou zero para cada rastreamento. Isso tem o efeito de mover o traço para cima ou para baixo na janela.
- A constante do filtro define a porcentagem da escala completa e pode ser positiva ou negativa.
O filtro de escala simplesmente multiplica todos os pontos de dados por uma porcentagem da escala completa. Isso tem o efeito de aumentar ou diminuir o tamanho de um rastreamento na janela.
- A constante de filtro define a porcentagem do valor original. Constantes menores que 100% reduzirão a amplitude do traço, enquanto constantes maiores que 100% aumentarão a amplitude do traço.
A frequência mediana é calculada para um bloco de amostras cujo comprimento é definido pela constante do filtro. Esse cálculo é repetido conforme necessário ao longo do traço e as frequências resultantes plotadas como uma série de linhas que conectam as frequências médias calculadas. Os seguintes passos são realizados:
- Um bloco de amostras definido pela constante do filtro é coletado e preenchido com zero até a potência mais próxima de 2.
- Uma função de janelas aplicada aos dados, conforme especificado pela seleção na parte inferior esquerda da janela Configurações. Consulte Usando funções de janelas da FFT para obter mais informações.
- É realizada uma FFT e, se selecionado, os filtros passa-alta da FFT são usados para remover DC e remover frequências muito baixas dos cálculos. Observe que um componente DC grande pode degradar seriamente a precisão do cálculo da frequência mediana.
- A magnitude da amplitude de cada frequência de saída FFT é elevada ao quadrado.
- A frequência mediana é determinada de modo que a área do gráfico de frequência quadrática da amplitude abaixo da frequência mediana seja a mesma que acima da frequência mediana, ou seja, existe potência igual em ambos os lados da frequência mediana.
- O processo é repetido para o próximo bloco de amostras.
A frequência média é calculada para um bloco de amostras cujo comprimento é definido pela constante do filtro. Esse cálculo é repetido conforme necessário ao longo do traço e as frequências resultantes plotadas como uma série de linhas que conectam as frequências médias calculadas. Os seguintes passos são realizados:
- Um bloco de amostras definido pela constante do filtro é coletado e preenchido com zero até a potência mais próxima de 2.
- Uma função de janelas aplicada aos dados, conforme especificado pela seleção na parte inferior esquerda da janela Configurações. Consulte Usando funções de janelas da FFT para obter mais informações.
- É realizada uma FFT e, se selecionado, os filtros passa-alta da FFT são usados para remover DC e remover frequências muito baixas dos cálculos. Observe que um componente DC grande pode degradar seriamente a precisão do cálculo da frequência média.
- Uma FFT é realizada e todas as frequências abaixo (frequência máxima / 50) Hz são rejeitadas; isso corresponde a 10Hz a 1000 amostras / segundo.
- A magnitude da amplitude de cada frequência de saída FFT é elevada ao quadrado.
- A frequência média da amplitude resultante ao quadrado em relação ao gráfico de frequência é determinada.
- O processo é repetido para o próximo bloco de amostras.
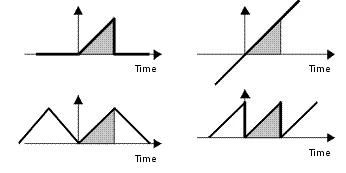
Quando os dados são capturados, uma 'janela' é efetivamente aberta no sinal para visualizar a forma de onda por um período antes que a 'janela' seja fechada novamente. Antes e depois da janela ser aberta, o cálculo da FFT não faz ideia do valor do sinal. Por exemplo, as quatro formas de onda mostradas à direita contêm os mesmos dados capturados (mostrados em cinza), mas com conteúdos de frequência diferentes.
Uma FFT assume que a sequência de dados faz parte de um sinal que se repete periodicamente, conforme ilustrado pela forma de onda dente de serra no canto inferior direito do diagrama acima. A consequência de assumir uma continuação periódica do sinal subjacente é que, se a amplitude no início e no final da amostra de dados não for igual, o sinal será analisado para conter uma descontinuidade, independentemente de o sinal ter ou não essa descontinuidade. . Como descontinuidades acentuadas têm amplos espectros de frequência, isso fará com que o espectro de frequências do sinal seja espalhado. A expansão significa que a energia do sinal que deve ser concentrada apenas em uma frequência, vaza para todas as outras frequências. Essa propagação de energia é chamada de "vazamento espectral". Como o vazamento espectral está relacionado a descontinuidades no final do tempo de medição, será pior para os sinais que caem, de modo que existem grandes descontinuidades.
Isso é um problema, pois a FFT será um cálculo preciso do conteúdo da frequência se os dados capturados forem um ou mais ciclos completos de um sinal subjacente periódico. Normalmente não é esse o caso.
Para melhorar a precisão da FFT, é prática comum multiplicar os dados amostrados por uma função de janela antes de implementá-la. Esta função da janela é uma série de números que geralmente são simétricos com o ponto médio do intervalo de tempo da amostra e têm um valor de ponto médio de um por exemplo a janela Triângulo ou Bartlett.

Muitas funções da janela são possíveis, incluindo uma Janela Retangular que não altera os dados. Algumas das funções da janela fornecidas são:
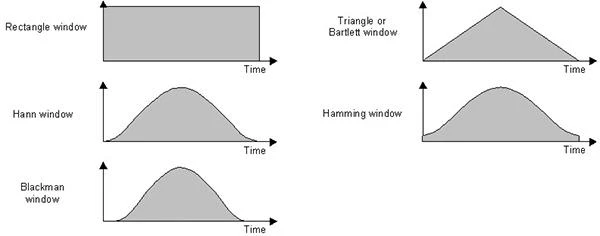
Para comparar as diferentes janelas, elas podem ser plotadas no mesmo eixo da seguinte maneira:
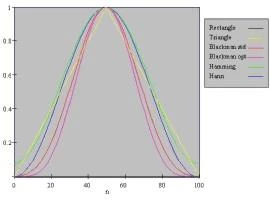
A escolha da função da janela geralmente é feita após alguma experiência no processamento do tipo de sinal usado. No entanto, algumas diretrizes podem ser dadas:
- Use uma janela retangular para sinais transitórios;
- Hann (von Hann) e Hamming para dados de formas de onda contínuas;
- Retangular (Flattop) para medições precisas de amplitude ou
- Blackman para resolução de frequência máxima
