EMGフィルタ
全てのウィンドウ内の全てのトレースに最大6つまでフィルタをかけることができます。元のデータは初めに有効なフィルタが適用されます。このフィルタからの出力データには次の有効フィルタが適用される、というように、最大6段階のフィルタを適用可能であり、表示されるのは最終フィルタからの出力データです。
全てのフィルタには以下のオプションがあります。
このフィルタは単純にマイナス値を同じ規模のプラス値に変換するものです。各フィルタの定数は不要です。
累加平均フィルタはどんな波形にも適用できます。
- このフィルタを有効にするとトレース上で計算したポイントは現時点までを含む値の平均になる
- 定数値の数は各フィルタで設定した定数値が適用され、さらに2つ以上のサンプルから設定できる
- 各フィルタの定数値はサンプルかミリ秒の中で指定。その際、ミリ秒はサンプル数×(1000÷サンプリングレート)と計算する
- 累加平均は入力と同じだけの出力を作成。例えば、各フィルタの定数値が3だとすると、以下の通り計算される
- o 出力1 = 入力1
- 出力2 =入力1と2の平均
- 出力3 = 入力1、2、3の平均
- 出力4 =入力2、3、4の平均
- 出力5 =入力3、4、5の平均
- 出力 n = n-2、n-1、nの平均
ヒント:平均フィルタは、波形内の高周波ノイズを減少させるのに役立ちます。例えば、サンプル数1000Hzでトレースした心拍数に50Hz 電源干渉が含まれている場合、1つの電源周波数(1/50秒)上で平均する事で減少できます。1つの電源周波数は 20のサンプル数に対応しているため (1000Hzサンプルレート÷ 50Hz interference)、20を平均するとノイズは大きく減少します。40、60、80…といったサンプル数でもノイズは減少しますが、同時に研究対象の信号も減少する可能性があります。
データの各サンプルは、初めに二乗した後、累加平均が計算されます。出力は計算した平均の二乗根になります。
- フィルタの定数値はサンプルかミリ秒の中で指定します。その際、ミリ秒はサンプル数×(1000÷サンプリングレート)と計算します。
速度フィルタは各データポイントでのデータ変化の速度を計算します。データ変化の速度は、その時点での接線の勾配です。
最適な勾配を得るためには、最小二乗法を使ってデータポイントの前後のデータを使い、直線を推定します。この線の勾配がフィルタされて出力されます。
- フィルタの定数値は、最小二乗の推定直線で使っているデータポイントの数を定義するもの。サンプルかミリ秒の中で指定。その際、ミリ秒はサンプル数×(1000÷サンプリングレート)と計算する
- フィルタを使用すると表示単位が変わる。例えば元の単位が度だとすると、フィルタ後は度/秒になる
融合フィルタは、グラフの面積の開始点から表示中のポイントまでを計算します。このフィルタを使うと、データがゼロ中心になっていない場合、急上昇/急降下のグラフになるケースがよく見られます。
- フィルタの定数値はデータポイントの計算エリアに対する割り算値を定義。この機能は、データからの融合出力が表示するには大きすぎる場合に便利
- このフィルタを使用すると表示単位が変わる。例えば元の単位が度だとすると、フィルタ後は度 - 秒になる
全てのデータポイントからフルスケールに対する割合分を足したり引いたりするフィルタです。各トレースの無効ポイントまたはゼロポイントを変えたり再設定する際に使用します。
- フィルタ定数値はフルスケールに対する割合を定義し、プラス、マイナスのどちらでも可能
中央値の周波数は、フィルタ定数値で長さが定義されたサンプル群に対して計算します。この計算はトレース全体にわたって繰り返され、その結果の周波数は線としてプロットされ、計算した中央値の周波数を連結します。この時、以下のような手順で進みます。
- フィルタ定数値で定義したサンプル群を抽出し、2の二乗に最も近い数字にゼロパディングされます
- 設定ウィンドウの左下で選択した内容に基づき、データに窓関数が適用される。FFT窓関数の記載をご参照
- FFTの実行。さらにFFTハイパスフィルタを選択していれば、計算からDCと超低周波が除去される。大きな直流成分があると中央値の周波数の計算精度が落ちる可能性があるので、注意したい
- 各FFT出力周波数の振幅規模は二乗される
- 中央値の周波数は、次のように定義される:中央値の周波数の下にある、振幅を二乗した周波数グラフの範囲は、中央値の周波数の上と同じ(例:中央値の周波数の両側は同じ電力)
- この手順は次のサンプル群にも繰り返される
平均周波数は、フィルタ定数値で長さ定義されたサンプル群に対して計算されます。この計算はトレース全体にわたって繰り返され、その結果の周波数は線としてプロットされ、計算した平均周波数を連結します。この時、以下のような手順で進みます。
- フィルタ定数値で定義したサンプル群を抽出し、2の二乗に最も近い数字にゼロパディング
- 設定ウィンドウの左下で選択した内容に基づき、データに窓関数が適用される。FFT窓巻子の記載をご参照
- FFTの実行。さらにFFTハイパスフィルタを選択していれば、計算からDCと超低周波が除去される。大きな直流成分があると平均周波数の算計算精度が落ちる可能性があるので、注意したい
- FFTが実行され、(最大周波数÷50)Hz以下の周波数は却下される。これは10Hzで1秒あたり1000サンプルに相当する
- 各FFT出力周波数の振幅規模は二乗される
- 周波数グラフと比較した振幅の二乗を計算して平均周波数が定義されます
- この手順は次のサンプル群にcorも繰り返される
データが取り込まれると、信号上にウィンドウが開いて波形を見ることができ、時間がたつとウィンドウが閉じます。ウィンドウが開く前及び開いた後、FFT計算は信号の値を認識していません。例えば、右に示した4つの波形は取り込まれた同じデータを含んでいますが(灰色で表示)、周波数は異なります。
FFTは、データシークエンスが信号の一部であり、上の図の右下にのこぎり波形で描いたように、定期的に繰り返すものと認識します。つまり、データサンプルの開始点・終了点においける振幅が同等でないと、信号が分析される際に、信号の連続有無にかかわらず連続停止という内容になります。信号間のギャップには幅広い周波数スペクトルがあるため、信号の周波数スペクトルが広がる事になります。広がるという事は、一つの周波数に集中するはずの信号エネルギーが他の周波数へ漏れ出すという現象であり、これをスペクトル漏れと呼びます。スペクトル漏れは、計測時刻の終了時での連続停止に関係していくるため、信号の大きなギャップはより悪い状況となります。
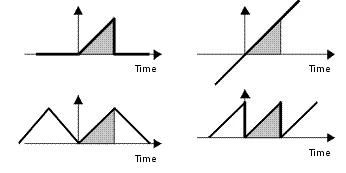
何故これが問題かというと、取り込んだデータが1つ以上のサイクルである場合のみ、FFTが正確な計算となるからです。通常はこのようなことはありません。
FFTの正確性を向上させるためには、FFTを適用させる前に窓関数でサンプルデータに掛け算するのが一般的です。この機能は、サンプル時間幅の中間点に対して対称な一連の数字であり、一つの窓(三角、バートレット等)の中間値を持つものです。

窓関数は、データに全く影響のない矩形窓等を含め、多数の種類が使用可能です。含まれている窓関数の例は:
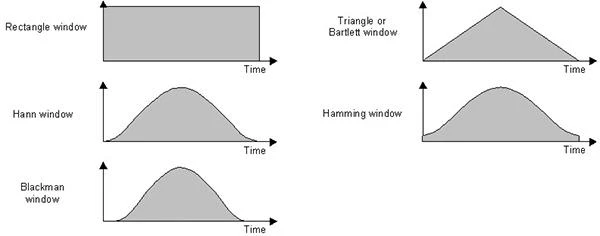
異なる窓を比較するために、以下のように同じ軸にプロットする事も可能です:
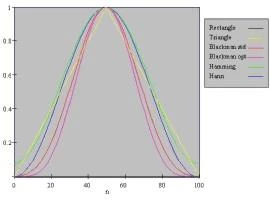
通常、窓関数の選択は、信号処理にある程度慣れたところで行いますが、以下のガイドラインを参考にしてみて下さい。
- 過渡信号には矩形窓を使う
- 連続波形データにはハン(フォンハン)またはハミング窓を使う
- 正確な振幅計測には、最大の周波数分解能を得るために、矩形窓(フラットトップ)またはブラックマンを使う
