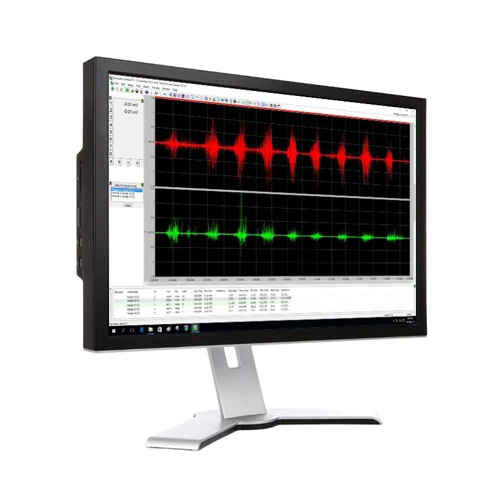
肌电图滤波器
每个滤波器具有以下选项:
该滤波器简单地将一个负值转换为一个相同幅值的正值。不需要任何常数。
一个移动的平均滤波器可被应用至任何波形。
- 启用时,在跟踪中计算出的各个点均为多个值直至(并包括)当前的点值的平均值。
- 这多个值的数目即为滤波器常数,并且可以从2个及以上的样本量开始设置。
- 滤波器常数可以由样本数或毫秒【毫秒数是由样本数值乘以(1000/采样率)】的数量来指定。
- 平均移动会产生与输入一样数量的输出。例如,假设滤波器常数为3时,会执行以下计算:
- 输出1 = 输入 1
- 输出 2 = 输入 1 和 2的平均值
- 输出 3 = 输入 1, 2 和 3的平均值
- 输出 4 = 输入 2, 3 和 4的平均值
- 输出 5 = 输入 3, 4 和 5的平均值
- 输出 n = 输入n-2, n-1 和 n的平均值
建议:平均滤波器在降低波形的高频噪音时是十分有用的。例如,如果一个在1000Hz采样的心跳跟踪包含50Hz的电源干扰,它可以通过平均超过1个电源周期(第1/50秒)来降低。一个电源周期对应20个样本量(1000Hz采样率通过50Hz的干扰),所以平均20个值将会明显地降低噪音。需要注意的是平均超过40, 60, 80…的样本也将减少噪音,但它还可能同时降低目标信号。
数据的每一个样本先被平方,然后会从这些平方数中取移动平均值。输出则为各个平均值的平方根。
- 滤波器常数可以由样本数或毫秒(毫秒数是由样本数值乘以(1000/采样率)的数量来指定。
速度滤波器可以在每个数据点计算数据的变化率。这是指该点切线的有效倾斜度。
为获得一个合适的倾斜度,会使用最小平方法来用数据每一侧所计算出的数据点来估计一条直线。而这条线的倾斜度则为该滤波器的输出。
- 该滤波器常数定义为最小平方法估计中使用的数据点的数值。它可以由样本数或毫秒(毫秒数是由样本数值乘以(1000/采样率)的数量来指定。
- 使用此滤波器会改变显示的单位。例如,如果原来的单位是度,那么滤波的单位则为度/秒。
集成滤波器会计算从开始直至当前显示的点下的区域面积。在数据没有集中于0时,该滤波器经常产生快速上升/下降曲线图。
- 该滤波器常数定义为一个除数,用于减少每一点的计算区域。这是十分有用的,否则会产生过大的集成输出而难以显示。
- 使用此滤波器会改变显示的单位。例如,如果原来的单位是度,那么滤波的单位则为度-秒。
抵消滤波器简单地为每一个数据点的满量程增加或减少一定的百分比。这可以被用于改变或重新定义每个跟踪里的无效点或零点。这具有在窗口中向上或向下移动轨迹的作用。
- 该滤波器常数定义为满量程的百分比,可以是正值或负值。
中频滤波器计算一批样品,其长度由该滤波器常数决定。该计算会必要地进行重复横跨轨迹,并将所得频率绘制成一系列连接计算中值频率的线。以下步骤将被执行:
- 通过滤波器常数定义的一批样本会被采集并零填充至最接近2的功率。
- 窗函数可以应用到数据,该数据是通过设置窗口左下角的选择功能指定的。更多信息请参阅FFT窗函数的使用。
- 通过选择,可以执行FFT,并且FFT高通滤波器被用于消除直流电,以从计算中移除非常低的频率。需要注意的是,大的直流分量会严重降低中值频率计算的准确性。
- 每个FFT输出的振幅频率都被平方。
- 中值频率被确定,使得中值频率下的振幅平方区域的频率图与其以上的相同,即中值频率的两侧都具有相等的功率。
- 该过程也会重复于下一批样本。
均值频率滤波器计算一批样品,其长度由该滤波器常数决定。该计算会必要地进行重复横跨轨迹,并将所得频率绘制成一系列连接计算均值频率的线。以下步骤将被执行:
- 通过滤波器常数定义的一批样本会被采集并零填充至最接近2的功率。
- 窗函数可以应用到数据,该数据是通过设置窗口左下角的选择功能指定的。更多信息请参阅FFT窗函数的使用。
- 通过选择,可以执行FFT,并且FFT高通滤波器被用于消除直流电,以从计算中移除非常低的频率。需要注意的是,大的直流分量会严重滴降低均值频率计算的准确性。
- 执行FFT时所有低于(最高频率/50)Hz的频率将被拒绝。这对应于10Hz的1000样本/秒。
- 每个FFT输出的振幅频率都被平方。
- 所得振幅平方的均值频率对频率曲线被确定。
- 该过程也会重复于下一批样本。
当数据被捕获时,会有效地针对该信号打开一个“窗口”来查看该信号在“窗口”再次关闭之前这段时期的波形。在窗口打开之前和关闭之后,FFT计算不出信号的值。例如,右边所示的4个波形包含相同的捕获数据(以灰色显示),但具有不同的频率内容。
FFT假设数据顺序是信号的一部分,且如上图右下角的锯齿波形图一样周期性地重复。假设底层信号有一段周期性延展的结果是,如果数据样本开始和结束的振幅不相等,不管信号是否确实具有不连续性,都将被分析为含有一个中断。由于明显的不连续性具有广阔的频谱,这些均会导致信号的频谱被传播出去。传播是指本应该只集中在一个频率中的信号能量泄漏到其他其他频率中去。这种能量的传播被称为“频谱泄露”。由于频谱泄露与测量时间结束时的不连续性有关,所以它会令信号下降更加严重,这样会导致很大的不连续。
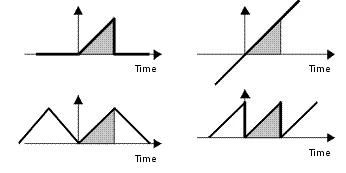
这个问题是因为FFT仅在捕获数据为周期性基础信号的一个或多个完整周期时才能够精准计算。但通常不是这样的情况。
为了改善FFT的准确性,通常的做法是将窗函数先乘以样本数据再进行FFT。该窗函数功能是一系列通常与采样时间范围中点对称的数值,并且该数值含有一个中点值为1。例如,三角函数或巴特利特窗口。

许多窗函数可能包含一个矩形窗,而该矩形窗不会真正改变数据。提供到的窗函数功能有:
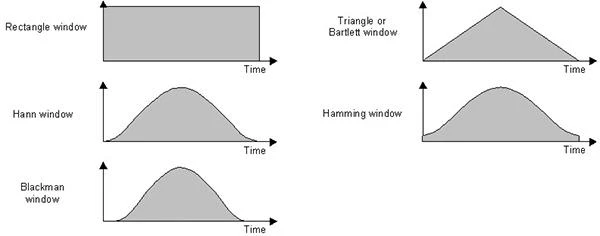
为了比较不同的窗口,它们可在同一轴线上被绘制如下:
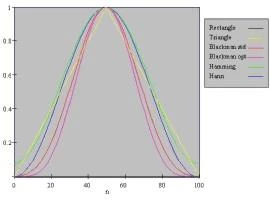
所使用的窗函数通常是在一些经验处理信号类型后选择的。然而,可以列出一些准则:
- 针对瞬态信号使用矩形窗。
- 针对连续波形数据使用Hann(von Hann)和Hamming窗。
- 针对精确幅度测量使用矩形(平顶)窗。
- 针对最大频率分辨率使用Blackman窗。